Right Angle Trigonometry

Side Length Ratios

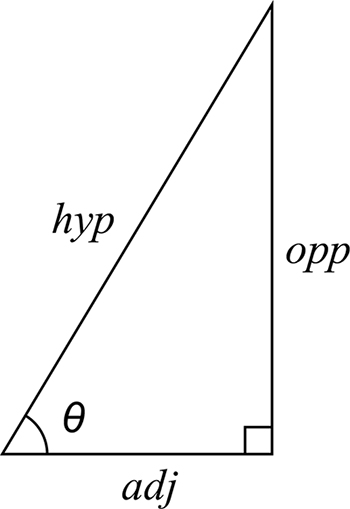
If $\theta$ is one of the two acute angles within a right-angled triangle, $\sin\theta$, $\cos\theta$ and $\tan\theta$ represent ratios of the triangle's side lengths (noting that adj, opp and hyp are the triangles adjacent, opposite and hypotenuse side lengths respectively).

$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}} \begin{align*}
\sin\theta &= \frac{opp}{hyp} &\quad\quad\quad \csc\theta &= \frac{hyp}{opp} \cr
\cos\theta &= \frac{adj}{hyp} &\quad\quad\quad \sec\theta &= \frac{hyp}{adj} \cr
\tan\theta &= \frac{opp}{adj} &\quad\quad\quad \cot\theta &= \frac{adj}{opp}
\end{align*}$$

The Laws of Sines and Cosines

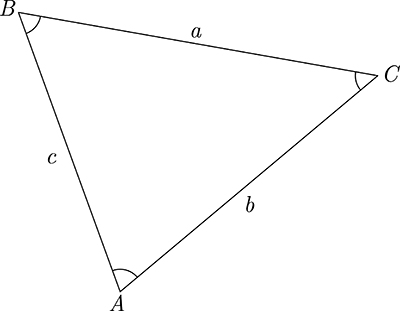
The law of sines and the law of cosines provide useful relationships between the side lengths a, b, c of any triangle and the triangle's internal angles A, B, C.

The law of sines

$$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$$

The law of cosines

$$\begin{align*} a^2 &= b^2+c^2-2bc\cos A\cr
b^2 &= a^2+c^2-2ac\cos B\cr
c^2 &= a^2+b^2-2ab\cos C \end{align*}$$