Fractions and Decimals

Fractions and decimals appear everywhere in construction and design-related problems. Whenever one quantity is broken down into a number of smaller quantities (e.g. a wall width divided into three equally-long sub-widths), the resulting smaller quantities represent fractions of the original. Fractions can be whole numbers, but in practice they are usually numbers that lie `between' whole numbers -- such as $1.75$, for example, which lies three quarters of the way between $1$ and $2$. Measurements that cannot be expressed as whole numbers are conventionally written in decimal notation.

$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}}$$

Example problem

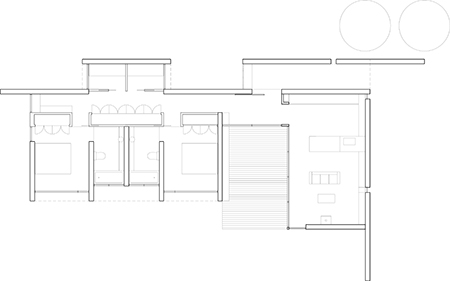
Floor Plan
The above image shows the floorplan of a single-story, four-bedroom house. The house has two identically-dimensioned main bedrooms with ensuites. For purposes of discussion, consider the Northernmost main bedroom / ensuite combination. This bedroom has floorspace dimensions $3000\;\ctext{mm} \times 3400\;\ctext{mm} = 10.2\;\ctext{m}^2$; its ensuite has dimensions $1500\;\ctext{mm} \times 3100\;\ctext{mm} = 4.65\;\ctext{m}^2$. Is the ensuite floor area more or less than half that of the bedroom? (Are there any `rules of thumb' in this regard?)

Solution

Written as a fraction, the ensuite floor area divided by the bedroom floor area is given by

$$\frac{\ctext{ensuite floor area}}{\ctext{bedroom floor area}}=\frac{4.65\;\ctext{m}^2}{0.20\;\ctext{m}^2}=4.65\;\ctext{m}^2\div 10.20\;\ctext{m}^2\approx 0.46$$

The rule of thumb is a half ($\frac{1}{2}$ or $0.5$).

For further information see this page in Maths Start (vUWS login required)