Trigonometry

$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}}$$

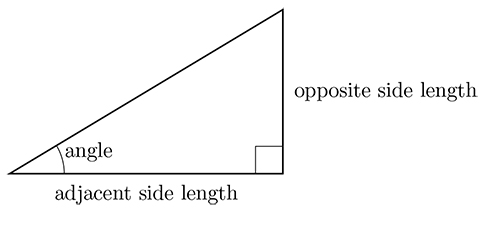
For many practical applications, trigonometry is concerned with triangles and the relationships between their side lengths and internal angles. For example, in the right-angled triangle shown in the figure below, the ratio of the length of the side opposite the indicated angle and the side adjacent to it is equal to $\tan\left(\ctext{angle}\right)$ ($\tan$ belongs to the same family of trigonometric functions as $\sin$ and $\cos$):$$\frac{\ctext{opposite side length}}{\ctext{adjacent side length}} = \tan(\ctext{angle}).$$

This formula is convenient because most scientific calculators have the standard trigonometric functions built in, and so, for example, an adjusted version of the above formula,

$$\ctext{opposite side length} = \ctext{adjacent side length} \times \tan\left(\ctext{angle}\right),$$can be used to calculate the length of the opposite side of a triangle when the length of the adjacent side and the angle between this side and the triangle's hypotenuse is given.

Example Problem

If the pitch angle of the roof shown in the figure below is to be $30$ degrees, and the rafter's run is to be $4000$ mm, calculate the rafter's rise (in millimetres)?

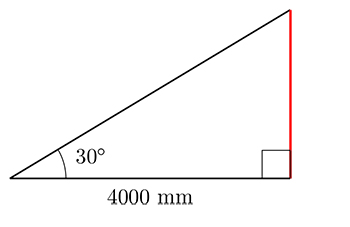
Solution

Using the formula above for calculating the opposite side length, we have
$$\ctext{opposite side length} = 4000\;\ctext{mm}\times \tan\left(30^\circ\right) \approx 4000\;\ctext{mm}\times0.57735 = 2309.4\;\ctext{mm}.$$

For more information see this page and this page from Improve Your Maths (student login required).