- Events, Workshops and Programs
- Resources by Discipline
- Support and Resources by Topic
- FYiMaths NSW
- About the MESH team
- Contact the MESH team
- MESH Research
- Resources for Staff
Basic Algebra
Usually, simple mathematical calculations -- such as dividing a number by two or adding two fractions together -- can be done without the use of abstract symbols such as $x$ and $y$. In more complicated mathematical calculations, however, the role of these symbols can be very useful, indispensable in fact. Algebra allows names to be given to unknown quantities in a calculation, and to thereby simplify the calculation and enable solutions to be found efficiently and rigorously.
$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}}$$
Example problem
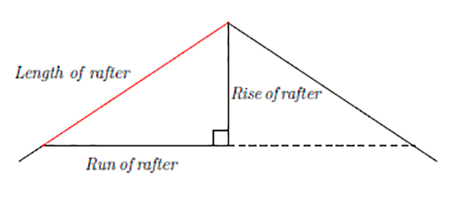
The above diagram shows the side view of a roof. Assuming the triangle formed by the rafter length and the rafter rise and run is right-angled, what is the length of the rafter in meters? (The rafter rise and run are $5.50\;\ctext{m}$ and $6.25\;\ctext{m}$ respectively.)
Solution
$$\ctext{Length of rafter}^2=\ctext{Rise of rafter}^2+\ctext{Run of rafter}^2$$
Instead of using words or phrases to denote specific quantities in a problem, it is usually more convenient to use letters. For example:
$$L=\ctext{Length of rafter},\;\;\; H=\ctext{Rise of rafter},\;\;\; W=\ctext{Run of rafter}.$$
In this case, the Pythagorean equation above becomes
$$L^2=H^2+W^2$$
This equation can be be used to find $L$ in terms of $H$ and $W$:
$$L = \sqrt{H^2 + W^2}= \sqrt{5.50^2+6.25^2}= \sqrt{30.25+39.0625}= \sqrt{69.3125}\approx 8.33m.$$
Further information can be found at this page in Maths Start (vUWS login required).
Mobile options:

