Tolerance and Error

$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}}$$

For many construction projects, pre-fabricated components such as concrete stairs, roof trusses or floor tiles, as well as industrial equipment such as compressed gas containers must be built to comply with measurement standards or tolerances specified by their design. For example, a concrete manufacturer might guarantee that the cement content of the mixes they supply will be as specified to within a tolerance of $1\%$ by volume. This means that the actual cement content of the mix supplied will not differ by more or less than $1\%$ of the specified content by volume. The difference between the actual and specified contents is known as the error.

Example Problem

The figure below gives the design for a feature wall to be built by assembling five polygonal steel panels. In order to ensure that the panels join smoothly to form the rectangular shape of the wall, the design specifies tolerances for the panels' side lengths of $2\;\ctext{mm}$. Assuming the panels are cut to this specification, what is the maximum possible error in the length of the top side of the wall?

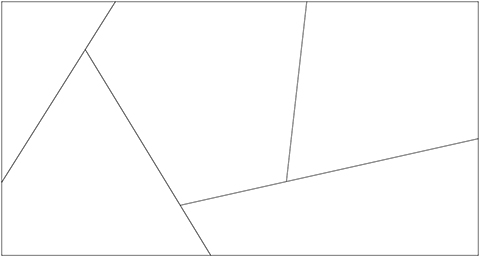
Solution

The maximum possible error will occur when each of the upper sides of the `top side' panels is $2\;\ctext{mm}$ overlong. Since there are three panels, the maximum error will be $3\times 2\;\ctext{mm} = 6\;\ctext{mm}$.

For more information see this BBC Bitewise page.