- Events, Workshops and Programs
- Resources by Discipline
- Support and Resources by Topic
- FYiMaths NSW
- About the MESH team
- Contact the MESH team
- MESH Research
- Resources for Staff
Area and Volume
$$\newcommand{\ctext}[1]{\style{font-family:Arial}{\text{#1}}}$$
When working with areas and volumes, precise calculations are only possible by use of formulae and methods for combining and applying these formulae. Common examples of formulae are the area of a circle (given by $\ctext{Area} = \pi r^2$, where $\pi\approx 3.14159$ and $r$ is the circle's radius), the surface area of a semi-sphere (given by $\ctext{Surface area} =2\pi r^2$, where $r$ is the sphere's radius), and the volume of a cylinder (given by $\ctext{Volume} = \pi r^2h$, where $r$ is the base circle's radius and $h$ is the cylinder's height). Areas and volumes of less familiar shapes and solids can be calculated using the calculus-based techniques of numerical integration, but for most practical purposes this is done using formulae and methods `behind the scenes' in programs such as Mathematica or Matlab. An example of combined use of formulae and a method is calculating the volume `trapped' between a cylinder and a cube that is wholly contained within the cylinder. The method is to subtract the volume of the cube from that of the cylinder.
Example problem
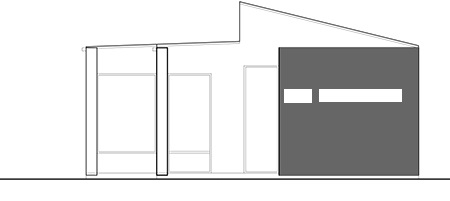
Solution
$$\begin{align*}
\ctext{Brick area}&=\ctext{Area of wall}-\left(\ctext{area of small window}+\ctext{Area of large window}\right)\cr
&=3.40\;\ctext{m}\times 3.40\;\ctext{m}-\left(0.70\;\ctext{m}\times 0.28\;\ctext{m}+ 1.75\;\ctext{m}\times 0.28\;\ctext{m}\right)\cr
&\approx 11.56\;\ctext{m}^2-\left( 0.20\;\ctext{m}^2+ 0.49\;\ctext{m}^2\right)\cr
&= 10.87\;\ctext{m}^2
\end{align*}$$
For more information see this page from Maths is Fun or this page from Waybuilder
Mobile options:

