Vector Operations
Vectors and Scalars
A vector is a quantity that has both a magnitude (or size) and a direction. For example, velocity. Velocity is a speed in a particular direction. So, although speed is a scalar quantity as it has only magnitude, velocity is a vector.
An example of another vector quantity is a displacement. This tells us how far away we are from a fixed point, and it also tells us our direction relative to that point.
Examples of other vector quantities are: acceleration due to gravity of the earth in a given place, force exerted on an object.
A scalar quantity consists of magnitude, but no direction. Examples of scalar quantities are: distance, speed, length, mass and time.
Representation of vector and scalar quantities
Vectors are represented in diagrams by using lines with arrows indicating the direction. For example, in the figure below, the vector shown is denoted by $\overrightarrow{AB}$, and is pronounced as “the vector AB”.

Line showing vector from A to B.
The magnitude of $\overrightarrow{AB}$ is the length of segment $AB$, and is represented by the symbol $|\overrightarrow{AB}|$. For example, if $\overrightarrow{AB}$ is the velocity of a vehicle, then $|\overrightarrow{AB}|$ is the speed of the vehicle. Sometimes a vector is represented with a small letter such as $\mathbf{a}$, in a bold typeface. However, in writing, we normally put a bar underneath, or sometimes on top of, the letter such as $\overline{a}$ or $\underline{a}$. The magnitude of vector $\mathbf{a}$ is written as $a$ or as $|\mathbf{a}|$ . The two-parallel vectors $\mathbf{a}$ and $\mathbf{b}$ are represented as $\mathbf{a} || \mathbf{b}$.
Vector addition and subtraction
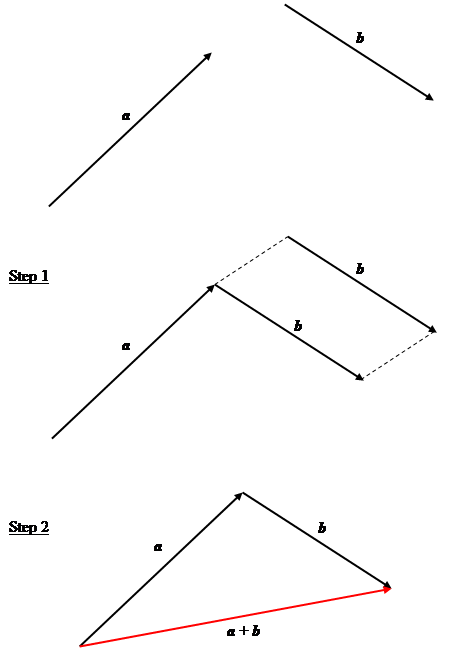
Steps showing addition of two vectors $\mathbf{a}$ and $\mathbf{b}$
In the example given in the figure above, the sum $\mathbf{a} + \mathbf{b}$ of the given vectors $\mathbf{a}$ and $\mathbf{b}$ is given by the triangle rule. According to this rule,
In step 1, vector $\mathbf{b}$ is shifted without changing its length and direction until it touched the head of $\mathbf{a}$.
In step 2, the vector $\mathbf{a} + \mathbf{b}$ is equal to the vector that begins with the tail of $\mathbf{a}$ and ends at the head of $\mathbf{b}$.
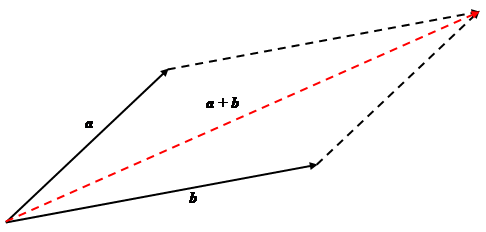
Vector addition using parallelogram law
There is another law called the parallelogram law for vector addition. According to this law, instead of making the second vector start where the first one finishes, we make them both start at the same place, and complete a parallelogram as shown in the figure above.
It gives the same result as the triangle law, because one of the properties of a parallelogram is that opposite sides are equal and in the same direction, so that $\mathbf{b}$ is repeated at the top of the parallelogram.
Subtraction of two vectors is performed by addition of negative vectors as shown in the figure below. For example: $\mathbf{a} - \mathbf{b} = \mathbf{a} + (- \mathbf{b})$
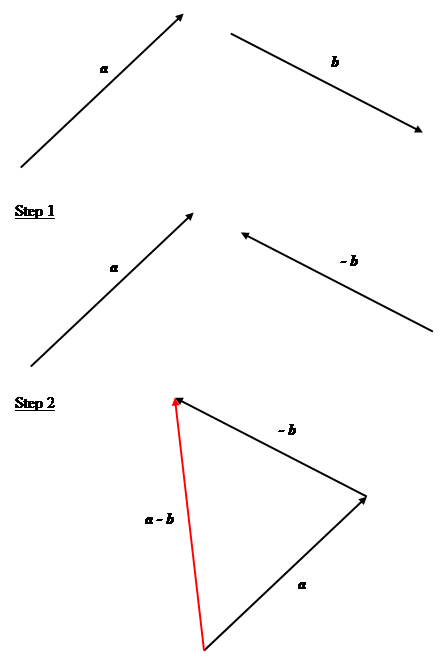
Subtraction of vector $\mathbf{b}$ from vector $\mathbf{a}$
Unit vectors
For a vector $\mathbf{a}$, a unit vector in the direction of $\mathbf{a}$ is represented as $\mathbf{\hat{a}}$. A unit vector is a vector whose length is 1 such that $|\mathbf{\hat{a}}|=1$. So, we can express vector $\mathbf{a}$ as $$\mathbf{a} = a\;\mathbf{\hat{a}}.$$
Here, $\mathbf{\hat{a}}$ has a magnitude of 1 and $a$ is the magnitude of $\mathbf{a}$ so that $a=|\mathbf{a}|$. Then, unit vector $\mathbf{\hat{a}}$ can be represented as $$\mathbf{\hat{a}} = \frac{\mathbf{a}}{a} =\frac{\mathbf{a}}{|\mathbf{a}|}$$
Cartesian components of a vector
Besides representing vectors in terms of position of the terminal point relative to the initial point (as shown in the previous section), they can be represented in cartesian axes as well. In cartesian axis, vectors can be used to specify the coordinates of a point relative to the axes.
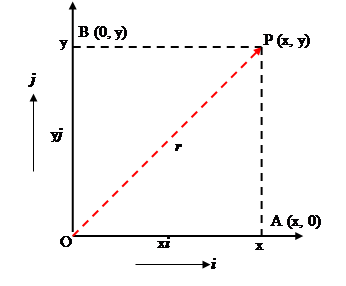
Position vector $\mathbf{r}$ of point P (x, y).
Consider the two-dimensional case as shown in the figure above. Here, two unit vectors $\mathbf{i}$ and $\mathbf{j}$ are represented as unit vectors in directions $x$ and $y$ respectively. So, $$\overrightarrow{OA}=x\mathbf{i},\quad \overrightarrow{OB}=y\mathbf{j}.$$
Then, $$\mathbf{r}=\overrightarrow{OA}+\overrightarrow{OB}=x\mathbf{i}+y\mathbf{j}.$$
And, from Pythagoras theorem, $$|\mathbf{r}|=\sqrt{x^2+y^2}.$$
This holds true for three dimensions as well, where$|\mathbf{r}|$ will be given by $$|\mathbf{r}|=\sqrt{x^2+y^2+z^2}$$
and $\mathbf{r}$ is given by $$\mathbf{r}=x\mathbf{i}+y\mathbf{j} +z\mathbf{k}$$
where $\mathbf{k}$ is a unit vector in the direction of the $z$ axis.
Dot or scalar product
The dot or scalar product of two vectors $\mathbf{a}$ and $\mathbf{b}$ is defined as $$\mathbf{a}\cdot\mathbf{b}=|\mathbf{a}| |\mathbf{b}|\cos\theta$$
where
$|\mathbf{a}|=$ magnitude of vector $\mathbf{a}$
$|\mathbf{b}|=$ magnitude of vector $\mathbf{b}$
$\theta =$ angle between vectors $\mathbf{a}$ and $\mathbf{b}$
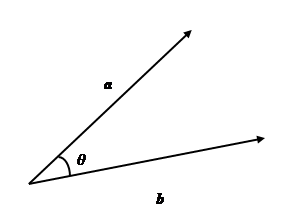
Two vectors $\mathbf{a}$ and $\mathbf{b}$ at an angle $\theta$
Some properties of the scalar product
CommutativityThe scalar product gives the same result whichever way around we perform the calculation $$\mathbf{a}\cdot\mathbf{b} = \mathbf{b}\cdot\mathbf{a}$$
Distributivity
The scalar product is distributive over vector addition $$\begin{align*}\mathbf{a}\cdot (\mathbf{b} + \mathbf{c})&=\mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\\ (\mathbf{b} + \mathbf{c})\cdot \mathbf{a} &=\mathbf{b}\cdot\mathbf{a}+\mathbf{c}\cdot\mathbf{a}\end{align*}$$
Scalar product of two perpendicular vectors
The scalar product of two vectors which are at right-angles is always 0. These vectors are called perpendicular or orthogonal. That is two vectors $\mathbf{a}$ and $\mathbf{b}$ are perpendicular if and only if $$\mathbf{a}\cdot\mathbf{b} = 0.$$
Scalar product of two vectors in cartesian form
If $\mathbf{i}$, $\mathbf{j}$ and $\mathbf{k}$ are unit vectors in the directions of the $x$, $y$ and $z$ axes, then $$\begin{align*} \mathbf{i}\cdot\mathbf{j}=\mathbf{i}\cdot\mathbf{k}= \mathbf{j}\cdot\mathbf{k}&=0\\ \mathbf{i}\cdot\mathbf{i}=\mathbf{j}\cdot\mathbf{j}=\mathbf{k}\cdot\mathbf{k}&=1\end{align*}$$
This means that if $\mathbf{a} = a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k}$ and $\mathbf{b} = b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k}$ then $$\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3.$$
Cross or vector product
The vector product of two three dimensional vectors $\mathbf{a}$ and $\mathbf{b}$ is defined as $$\mathbf{a}\times\mathbf{b}=|\mathbf{a}| |\mathbf{b}|\sin\theta\;\mathbf{\hat{n}}$$
where
$|\mathbf{a}|=$ magnitude of vector $\mathbf{a}$
$|\mathbf{b}|=$ magnitude of vector $\mathbf{b}$
$\theta =$ angle between vectors $\mathbf{a}$ and $\mathbf{b}$
$\mathbf{\hat{n}}=$ unit vector perpendicular to both $\mathbf{a}$ and $\mathbf{b}$ whose direction is given by the right hand screw rule.

The direction of vector product determined by right hand screw rule.
The right hand screw rule means that we imagine a screwdriver in the right hand. The direction of the vector product is the direction in which a screw would advance as the screwdriver handle is turned in the sense from $\mathbf{a}$ to $\mathbf{b}$.
Some properties of the vector product
Non-commutativity
The vector product is non-commutative contrary to scalar product which means that the order in which we do the calculation does matter. $$\mathbf{a}\times \mathbf{b}=-\mathbf{b}\times\mathbf{a}$$
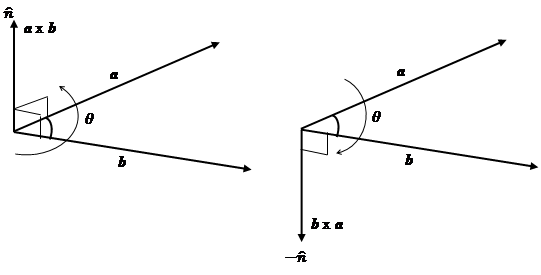
Direction of $\mathbf{a}\times \mathbf{b}$ and $\mathbf{b}\times\mathbf{a}$ are opposite.
Distributivity
The vector product is distributive over addition similar to the scalar product. $$\begin{align*}\mathbf{a}\times (\mathbf{b} + \mathbf{c})&=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}\\ (\mathbf{b} + \mathbf{c})\times \mathbf{a} &=\mathbf{b}\times\mathbf{a}+\mathbf{c}\times\mathbf{a}\end{align*}$$
Vector product of two parallel vectors
The vector product of two vectors which are parallel to each other is always $\mathbf{0}$. $\mathbf{0}$ is called the zero vector. If $\mathbf{a}$ and $\mathbf{b}$ are parallel vectors (have the same direction) then $$\mathbf{a}\times\mathbf{b} = 0.$$
Vector product of two vectors in cartesian form
If $\mathbf{i}$, $\mathbf{j}$ and $\mathbf{k}$ are unit vectors in the directions of the $x$, $y$ and $z$ axes, then $$\begin{align*} \mathbf{i}\times\mathbf{j}&=\mathbf{k}\\ \mathbf{k}\times\mathbf{i}&= \mathbf{j}\\ \mathbf{j}\times\mathbf{k}&=\mathbf{i}\\ \mathbf{i}\times\mathbf{i}=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k}&=\mathbf{0}\end{align*}$$
Additional Resources
- Introduction to Vectors - this PDF from mathcentre.ac.uk expands on the information given above.
- Vectors - another introduction to vectors with several examples (free signup required to view full document).
- Vector Products - further information on the vector product with examples.
- Vectors in Physics - a video discussing the use of vectors in physics
- Vectors and Scalars - a Khan Academy video examining the differences between vector and scalar quantities.
Mobile options:

