Trigonometry
Pythagoras' theorem
In a right-angled triangle, the area of the square on the hypotenuse is equal to sum of the areas of the squares on the two shorter sides.
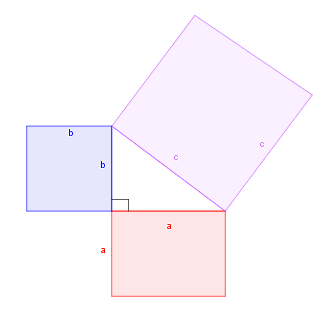
In the above triangle $$\begin{align*} \text{Square on side a}+\text{Square on side b}&=\text{Square on side c}\\ {\color{red}{a}}^2+{\color{blue}{b}}^2&={\color{#cc0099}{c}}^2 \end{align*}$$
Trigonometric ratios in a right-angled triangle
With reference to the following following diagram:
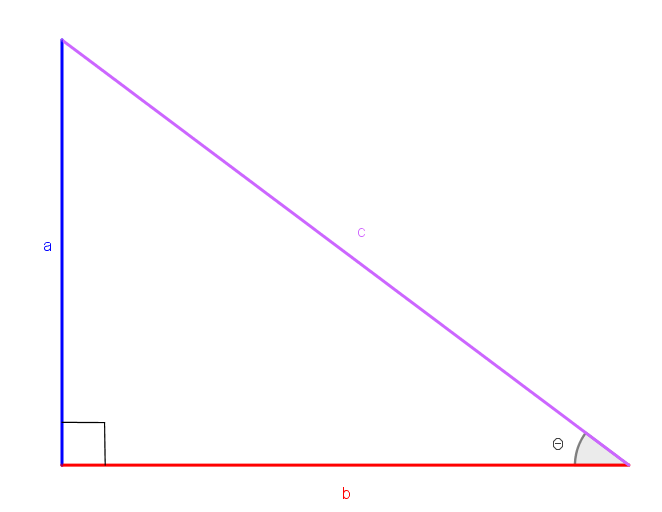
The tangent of the given angle $\theta$ is given as $$\tan\theta=\frac{{\color{blue}{\text{opposite}}}}{{\color{red}{\text{adjacent}}}}=\frac{{\color{blue}{a}}}{{\color{red}{b}}}$$
The sine of the given angle $\theta$ is given as $$\sin\theta=\frac{{\color{blue}{\text{opposite}}}}{{\color{#cc0099}{\text{hypotenuse}}}}=\frac{{\color{blue}{a}}}{{\color{#cc0099}{c}}}$$
The cosine of the given angle $\theta$ is given as $$\cos\theta=\frac{{\color{red}{\text{adjacent}}}}{{\color{#cc0099}{\text{hypotenuse}}}}=\frac{{\color{red}{b}}}{{\color{#cc0099}{c}}}$$
Some common angles and their trigonometric ratios
| Angle ($\theta$) | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|
| $0^\circ$ | $0$ | $1$ | $0$ |
| $30^\circ$ | $\frac12$ | $\frac{\sqrt3}{2}$ | $\frac{1}{\sqrt3}$ |
| $45^\circ$ | $\frac{1}{\sqrt2}$ | $\frac{1}{\sqrt2}$ | $1$ |
| $60^\circ$ | $\frac{\sqrt3}{2}$ | $\frac12$ | $\sqrt3$ |
| $90^\circ$ | $1$ | $0$ | $\infty$ |
Equivalent angles in degrees and radians
$$\begin{align*} 360^\circ &=2\pi\text{ radians}\\ 180^\circ &=\pi\text{ radians}\\ 90^\circ &=\frac{\pi}{2}\text{ radians}\\ 45^\circ &=\frac{\pi}{4}\text{ radians}\\ 30^\circ &=\frac{\pi}{6}\text{ radians}\end{align*}$$
Some trigonometric identities
$\newcommand{\cosec}{\operatorname{cosec}}$
$$\begin{align*} \sin^2\theta +\cos^2\theta &= 1 \\ \tan^2\theta + 1 &=\sec^2\theta\\ \cot^2\theta+1&=\cosec^2\theta\end{align*}$$
Triangle formulae
The cosine formula
When given three sides of a triangle, as shown below, we can find the angles using the cosine formula $$\begin{align*}{\color{red}{\cos A}}&=\frac{{\color{#cc0099}{b^2}}+{\color{blue}{c^2}}-{\color{red}{a^2}}}{2{\color{#cc0099}{b}}{\color{blue}{c}}}\\{\color{#cc0099}{\cos B}}&=\frac{{\color{blue}{c^2}}+{\color{red}{a^2}}-{\color{#cc0099}{b^2}}}{2{\color{blue}{c}}{\color{red}{a}}}\\{\color{blue}{\cos C}}&=\frac{{\color{red}{a^2}}+{\color{#cc0099}{b^2}}-{\color{blue}{c^2}}}{2{\color{red}{a}}{\color{#cc0099}{b}}}\end{align*}$$
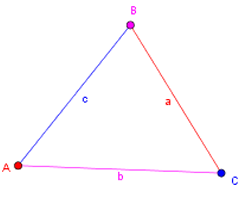
The sine formula
We can use the sine formula to find a side given two sides and an angle which is not included between the given sides: $${\color{red}{\frac{a}{\sin A}}}={\color{#cc0099}{\frac{b}{\sin B}}}={\color{blue}{\frac{c}{\sin C}}}$$
The area of a triangle
In the triangle above, if two sides and an included angle are known, the area of the triangle can be found using the appropriate formula below: $$\begin{align*} \text{Area}=\frac12{\color{red}{a}}\;{\color{#cc0099}{b}}\;{\color{blue}{\sin C}}\\\text{Area}=\frac12{\color{#cc0099}{b}}\;{\color{blue}{c}}\;{\color{red}{\sin A}}\\\text{Area}=\frac12{\color{blue}{c}}\;{\color{red}{a}}\;{\color{#cc0099}{\sin B}}\end{align*}$$
If the angles are unknown and the three sides are known, the area can be determined using the formula $$\text{Area}=\sqrt{s(s-{\color{red}{a}})(s-{\color{#cc0099}{b}})(s-{\color{blue}{c}})}$$ where,$$s=\frac{{\color{red}{a}}+{\color{#cc0099}{b}}+{\color{blue}{c}}}{2}$$
The addition formulae
$$\begin{align*}\sin (a\pm b)&=\sin a\cos b\pm \cos a\sin b\\ \cos (a\pm b)&=\cos a\cos b\mp \sin a\sin b\\ \tan (a\pm b)&=\frac{\tan a\pm \tan b}{1\mp \tan a\tan b}\end{align*}$$
Double angle formulae
Additional Resources
- Trigonometry - a set of pages from mathtutor.ac.uk covering all of the above plus exercises.
- Basic Trigonometry - a Khan Academy video introducing the the trig ratios.
- Basic Trigonometry - another explanation of the trig ratios from mathbff.
- Right Triangles - another video from mathbff explaining how to solve right triangles.
Mobile options:

