Plane Geometry
Similar Triangles
Triangle $ABC$ is said to be similar to triangle $PQR$, written $\triangle ABC \sim \triangle PQR$, if and only if one of the following equivalent conditions is satisfied:
- $AB:BC:CA=PQ:QR:RP$
- $\angle ABC =\angle PQR,\; \angle ACB=\angle PRQ,\; \angle BAC =\angle QPR$
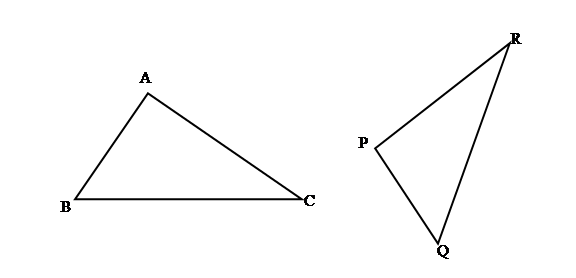
Two similar triangles $ABC$ and $PQR$
Area of plane shapes
a. Area of triangle $=\frac12\times b\times h$

Here, $h =$ vertical height and $b =$ base.
b. Area of rectangle $=w\times h$

Here, $w =$ width and $h =$ height.
c. Area of trapezium or trapezoid $=\frac12 \left( a+b\right) \times h$

Here, $a =$ base 1, $b =$ base 2 and $h =$ height
d. Area of circle $=\pi r^2$
Circumference of circle $=2\pi r$
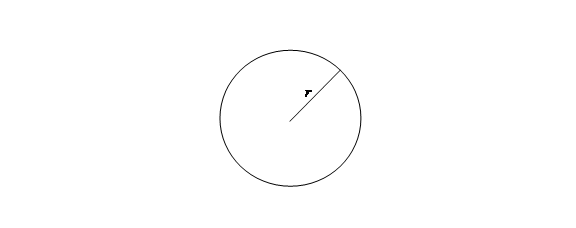
Here $r =$ radius of circle.
e. Area of ellipse $=\pi ab$
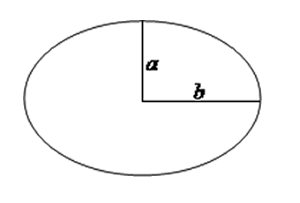
Here $a =$ semi minor axis and $b = $ semi major axis.
f. Area of sector $=\frac12 \times r^2 \times \theta$
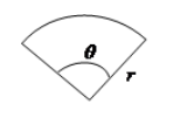
Here $r =$ radius and $\theta =$ angle in radians.
Types of angles
Besides common types of angles such as acute angle, right angle, obtuse angle, straight angle and reflex angle, some other types of angles are as follows:
a. Congruent angles
Two angles which have same angle are known as congruent angles.

Here $\angle ABC$ and $\angle PQR$ are congruent angles.
b. Angles around a point
The sum of angles around a point is always $360^\circ$.

Here $\angle AOB+\angle BOC+\angle COD+\angle DOA = 360^\circ$.
c. Adjacent Angles
Angles which have a common side and common vertex (corner point) and which do not overlap are known as adjacent angles.
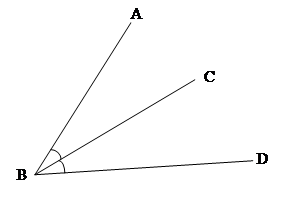
Here, $\angle ABC$ and $\angle CBD$ share common vertex $B$ and common side $BC$ and they are not overlapping. So, $\angle ABC$ and $\angle CBD$ are adjacent angles.
d. Supplementary angles
Two angles are supplementary when their sum is equal to $180^\circ$.

Here, supplementary angles $\angle ABC + \angle CBD = 180^\circ$.
e. Complementary angles
Two angles are complementary when their sum is equal to $90^\circ$.

Here, complementary angles $\angle ABC + \angle CBD = 90^\circ$.
f. Angles made by transversal crossing parallel lines
A transversal is a line that crosses at least two other lines. When a transversal crosses parallel lines, many angles are formed. For example, when transversal $XY$ crosses parallel lines $AB$ and $CD$ at point $P$ and $Q$.

Vertically opposite angles
$\angle APX = \angle QPB = a \quad \angle CQP = \angle DQY = a$
$\angle XPB = \angle APQ = b \quad \angle PQD = \angle CQY = b$.
Alternate interior angles
$\angle BPQ = \angle CQP = a$.
$\angle APQ = \angle PQD = b$.
Alternate exterior angles
$\angle APX = \angle DQY = a$.
$\angle XPB = \angle CQY = b$.
Corresponding angles
$\angle APX = \angle CQP = a \qquad \angle QPB = \angle DQY = a$.
$\angle XPB = \angle PQD = b \qquad \angle APQ = \angle CQY = b$.
Additional Resources
Problems in Plane and Solid Geometry - this e-book contains an enormous number of problems in geometry and goes far in advance of what is presented here.
Introduction to Basic Geometry - a solid theoretical introduction to Euclidean geometry.
High School Geometry - this series of videos from the Khan Academy will give you a solid grounding in geometry.
Introduction to Geometry - the first of a series of videos from MathFortress.
Mobile options:

