Analytic Geometry
Cartesian coordinates
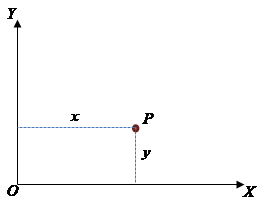
In the Cartesian coordinate system, a point $P$ is given by two mutually perpendicular distances $x,\; y$ (coordinates) measured from two mutually perpendicular axes $X,\; Y$ (coordinate axes) intersecting at the origin $O$.
Polar coordinates
In the polar coordinate system, a point $P$ is given by two polar coordinates associated with a fixed axis $X$ (polar axis) and a fixed point $O$ on the axis (pole). The first coordinate is the radius $r$, the distance from $O$ to $P$, and the second coordinate is the position angle $\theta$, measured from $X$ to $r$.

Relationship between Cartesian and polar coordinates
| Cartesian coordinates | Polar coordinates | |
|---|---|---|
| Cartesian coordinates | $$x=x$$ $$y=y$$ | $$x=r\cos\theta$$ $$y=r\sin\theta$$ |
| Polar coordinates | $$r=\sqrt{x^2+y^2}$$ $$\theta =\tan^{-1}\left(\frac{y}{x}\right)$$ | $$r=r$$ $$\theta = \theta$$ |
Distance between two points
Cartesian coordinates
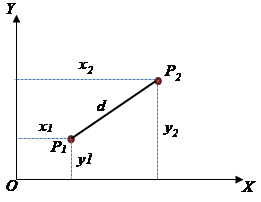
The distance between the points $P_1=(x_1, y_1)$ and $P_2=(x_2, y_2)$ is given by $$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}.$$
Polar coordinates

The distance between the points $P_1=(r_1, \theta_1)$ and $P_2=(r_2, \theta_2)$ is given by $$d=\sqrt{r_1^2+r_2^2-2r_1r_2\cos (\theta_1-\theta_2)}.$$
The Circle
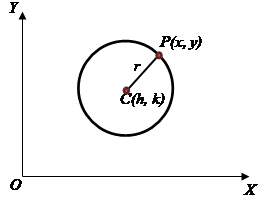
From the distance formula, the radius of the circle is given by $$\sqrt{(x-h)^2+(y-k)^2}=r$$
Squaring both sides gives $$(x-h)^2+(y-k)^2=r^2$$
which is the general equation of a circle with centre $(h,k)$ and radius $r$.
Lines

Slope of a line
The slope of the line that passes through the points $P_1=(x_1, y_1)$ and $P_2=(x_2, y_2)$ is given by $$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$$
Point-slope form of the equation of a line
From the above equation, the point-slope form of the equation of a line is derived as $$y-y_1=m(x-x_1)$$
Slope-intercept form of the equation of a line
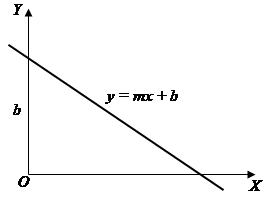
The equation of a line with slope $m$ and $y$-intercept $b$ is given by $$y=mx+b$$
Parallel and perpendicular lines
Two non vertical lines are parallel if and only if the have the same slope, that is $$m_1=m_2.$$
Two lines with slopes $m_1$ and $m_2$ are perpendicular if and only if $$m_1m_2=-1.$$
Additional Resources
- Analytic Geometry - a series of videos and quizzes from the Khan Academy on analytic geometry.
- Review of Analytic Geometry - pages from Stuart's text Essential Calculus - Early Trancendentals with questions and solutions.
- Analytic Geometry - lecture notes and exercises covering more detail than that presented here.
Mobile options:

