Linear Equations
System of linear equations
A linear equations in variables $x_1, x_2, x_3, \dots , x_n$ is an equation of the form $$a_1x_1+a_2x_2+a_3x_3+\dots +a_nx_n=b$$ where $a_1, a_2, a_3, \dots , a_n$ and $b$ are constant real or complex numbers. The constant $a_i$ is called the coefficient of $x_i$ and $b$ is called the constant term of the equation.
A system of linear equations is a finite collection of linear equations in the same variables. For example, a linear system of $m$ equations in $n$ variables $x_1, x_2, x_3, \dots , x_n$ can be written as $$\begin{align*}a_{11}x_1+a_{12}x_2+a_{13}x_3+\dots +a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+a_{23}x_3+\dots +a_{2n}x_n=b_2\\ \vdots\\a_{m1}x_1+a_{m2}x_2+a_{m3}x_3+\dots +a_{mn}x_n=b_m\end{align*}$$
A solution of a system of linear equations is a tuple $(s_1, s_2, \dots , s_n)$ of numbers that make each equation in the system a true statement when the values of $s_1, s_2, \dots , s_n$ are substituted for $x_1, x_3, \dots , x_n$ respectively. The set of all solutions of a linear system is called the solution set of the system. In order for a system of equations to have a unique solution we must have $m\ge n$, this does not guarantee the existence of a solution but is a necessary condition.
Solving systems of equations
There are several ways of solving systems of equations. We will give examples of three methods which are useful for small numbers of equations.
Graphical method
To find a solution to a set of equations graphically, we graph the equations and find the intersection point. For example, suppose that $$\begin{align}y&=2x+2\\y&=x-1\end{align}$$ we graph the equations in the coordinate plane
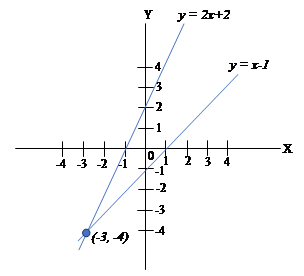
and note that the two lines intersect at $(-3, -4)$ which is the solution to this system of equations. Note that this method of solution is only useful for two equations in two unknowns.
Substitution method
In this method we solve one equation in terms of the other variable and substitute this into the other equation. For example, using equations (1) and (2) from above we can substitute $y$ from equation (1) directly into equation (2). $$\begin{align*}y&=x-1\\(2x+2)&=x-1\\2x-x&=-1-2\\x&=-3\end{align*}$$ The value of $x$ can them be used to find $y$ by substituting $x$ into either of the original equations. $$\begin{align*}y&=-3-1\\y&=-4\end{align*}$$
Elimination method
For this method we multiply one or both equation by a constant and then add or subtract the equations in order to eliminate one of the variables. For example, suppose $$\begin{align}2x+3y&=8\\3x+2y&=7\end{align}$$
We will eliminate the $x$ variable, so multiply equation (3) by $3$ and equation (4) by $2$: $$\begin{align*}\text{Equation (3) becomes } 6x+9y&=24\\\text{Equation (4) becomes }6x+4y&=14\end{align*}$$
Subtract the second equation from the first: $$\begin{align*}6x+9y&=24\\-(6x+4t&=14)\\ \hline \\5y&=10\end{align*}$$
Solve this new equation for $y$: $$y=\frac{10}{5}=2$$
Substitute $y=2$ into either equation (3) or (4) and solve for $x$: $$\begin{align*} 2x+3(2)&=8\\2x&=8-6\\x&=1\end{align*}$$
Other methods
For more than two variables, several other techniques such as Gaussian Elimination, the Gauss Jordan Method or Cramer's Rule (see the Matrices page) can be used.
Additional Resources
- Linear Equations - an extended version of the material presented here from the Australian Mathematical Sciences Institute
- Notes on Linear Equations - more detailed notes including discussion of the other methods mentioned above
- Systems of Equations - includes all of the above plus linear inequalities.
Mobile options:

