Complex Variables

Complex numbers can be defined as ordered pairs $(x,y)$ of real numbers that are to be interpreted as points in the complex plane, with rectangular coordinates $x$ and $y$, just as real numbers $x$ are thought of as points on the real line. When real numbers $x$ are displayed as points $(x,0)$ on the real axis, it is clear that the set of complex numbers includes the real numbers as a subset. Complex numbers of the form $(0,y)$ correspond to points on the $y$ axis and are called pure imaginary numbers. The $y$ axis is then referred to as the imaginary axis.

A complex number $(x,y)$ is denoted by $z$ (see Fig 1) so that $$z=(x,y).$$

The real numbers $x$ and $y$ are known as the real and imaginary parts of $z$ and are written as $$\Re z=x,\;\Im z=y.$$

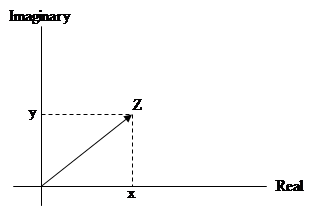
Fig 1: The Complex Plane

Two complex numbers $z_1=(x_1,y_1)$ and $z_2=(x_2,y_2)$ are equal whenever they have the same real parts and the same imaginary parts. thus, equal complex numbers correspond to the same point in the complex or $z$ plane.

Sum and product of two complex numbers

The sum $z_1+z_2$ of two complex numbers $z_1=(x_1,y_1)$ and $z_2=(x_2,y_2)$ is defined as $$(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2).$$

The product $z_1z_2$ of two complex numbers $z_1=(x_1,y_1)$ and $z_2=(x_2,y_2)$ is defined as $$(x_1,y_1)(x_2,y_2)=(x_1x_2-y_1y_2,y_1x_2+x_1y_2).$$

Any complex number $z=(x,y)$ can be written as $z=(x,0)+(0,y)$. Also $(0,y)$ can be written as $$(0,y)=(0,1)(y,0).$$ Hence, $$z=(x,0)+(0,1)(y,0).$$

If we consider a  real number as either $x$ or $(x,0)$ and let $i$ denote the imaginary number $(0,1)$, it is clear that $$z=x+iy$$ $$\text{where }i^2=(0,1)(0,1)=(-1,0)$$ $$\text{or }i^2=-1$$

The complex conjugate of a comples number $z=x+iy$ is defined as the complex number $x-iy$ and is denoted by \bar{z}. $$\bar{z}=x-iy$$

The number $\bar{z}$ is represented by the point $(x,-y)$ which is the reflection in the real axis of the point $(x,y)$ representing $z$ as shown in Fig 2.

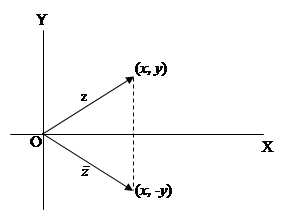
Fig 2: Complex conjugate of a complex number

Let $r$ and $\theta$ be the polar coordinates of the point $(x,y)$ that corresponds to a nonzero complex number $z=(x+iy)$. Since $x=r\cos \theta$ and $y=r\sin \theta$, the number $z$ can be written as $$z=r(\cos\theta+i\sin\theta)$$

The real number $\theta$ represents the angle, measured in radians, that $z$ makes with the positive real axis when $z$ is interpreted as a radius vector as shown in Fig 3.

Fig 3: Complex number in polar form

Complex numbers can be expressed in polar form by also giving the length of the arrow that represents the number and the angle between the arrow and the positive real axis. $$z=r\angle\theta$$

Complex numbers can be converted from polar to rectangular form, or vice versa, by using the fact that the magnitude of $z$, $|z|$, the real part $x$ and the imaginary part $y$ form a right triangle as shown in Fig 4.

Fig 4: Converting between polar and rectangular form

$$|z|=\sqrt{x^2+y^2}$$ $$\tan\theta=\frac{y}{x}$$ $$x=|z|\cos\theta$$ $$y=|z|\sin\theta$$

These equations can be used to convert numbers from polar to rectangular form or vice versa.

The Euler identities are given by $$\cos\theta=\frac{e^{i\theta}+e^{-i\theta}}{2}$$ $$\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2}$$

Another form of these identities is $$e^{i\theta}=\cos\theta +i\sin\theta$$ $$e^{-i\theta}=\cos\theta -i\sin\theta$$

Thus, $e^{i\theta}$ is a complex number having a real part of $\cos\theta$ and an imaginary part of $\sin\theta$. The magnitude is given by $$\left| e^{i\theta}\right|=\sqrt{\cos^2\theta+\sin^2\theta}$$

From the trigonometric identity $\cos^2\theta+\sin^2\theta =1$ we can conclude that $$\left| e^{i\theta}\right|=1$$

The angle of $e^{i\theta}$ is $\theta$ so we can write $$e^{i\theta}=1\angle\theta=\cos\theta +i\sin\theta.$$

A complex number such as $r\angle\theta$ can be written as $$r\angle\theta=r\times (1\angle\theta )=re^{i\theta}$$

$re^{i\theta}$ is the exponential form of a complex number.