Exponential and Logarithmic Functions
Exponential function
If $b$ is any fixed number such that $b>0$ and $b\ne 1$ then an exponential function is a function of the form $$f(x)=b^x$$ where $b$ is called the base and $x$ can be any real number.
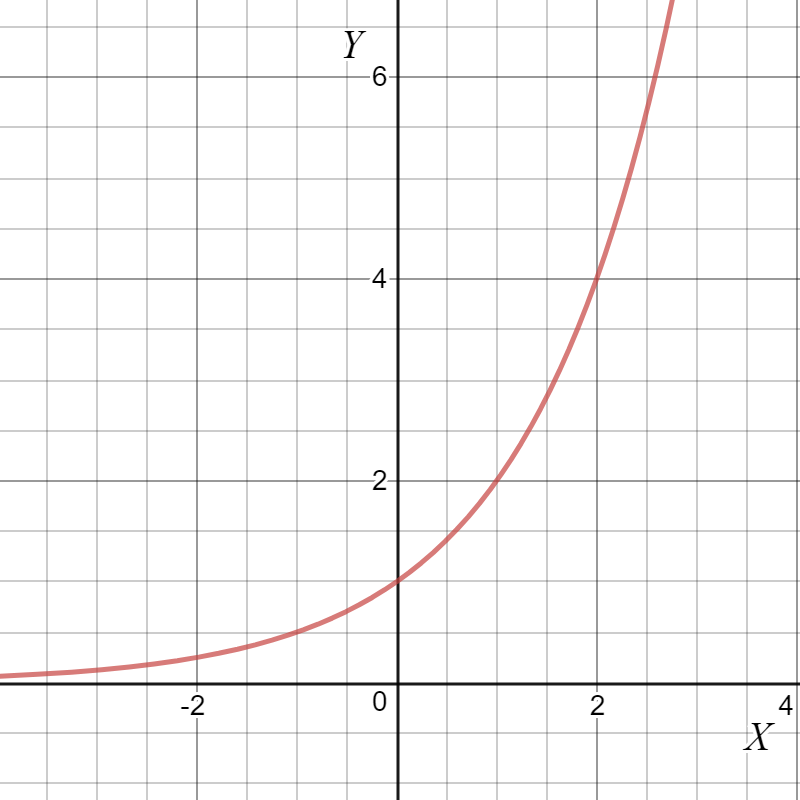
Fig 1: Graph of exponential function
The graph of $y=2^x$ is shown in Fig 1. The following common properties of exponential functions can seen from the graph:
- The graph of $b^x$ will always contain the point $(0,1)$.
- For every possible $b$ we have $b^x>0$.
- If $b > 1$ then the graph of $b^x$ will increase as $x$ increases (note that if $0 < b <1$, the graph of $b^x$ will decrease as $x$ increases).
- If $b^x = b^y$, then $x=y$.
An important base used in exponential functions is the base $e$ which is defined by $$e=\lim_{x\to\infty}\left(1+\frac1x\right)^x\approx 2.718281828.$$
$e$ is an irrational number which has important properties in many areas of engineering.
Logarithmic function
If $b$ is any fixed number such that $b>0$ and $b \ne 1$, and $x > 0$ is any positive real number, then a logarithmic function (with base $b$) is a function of the form $$y=\log_b x$$ which is equivalent to the exponential form $b^y=x$.
The inverse of an exponential function is a logarithmic function. The inverse of a function can be thought of as the function obtained by exchanging the $x$ and $y$ coordinates. This reflects the graph about the line $y=x$. As seen from the graph in Fig 2, the logarithmic curve (blue) is the reflection of the exponential curve (red).
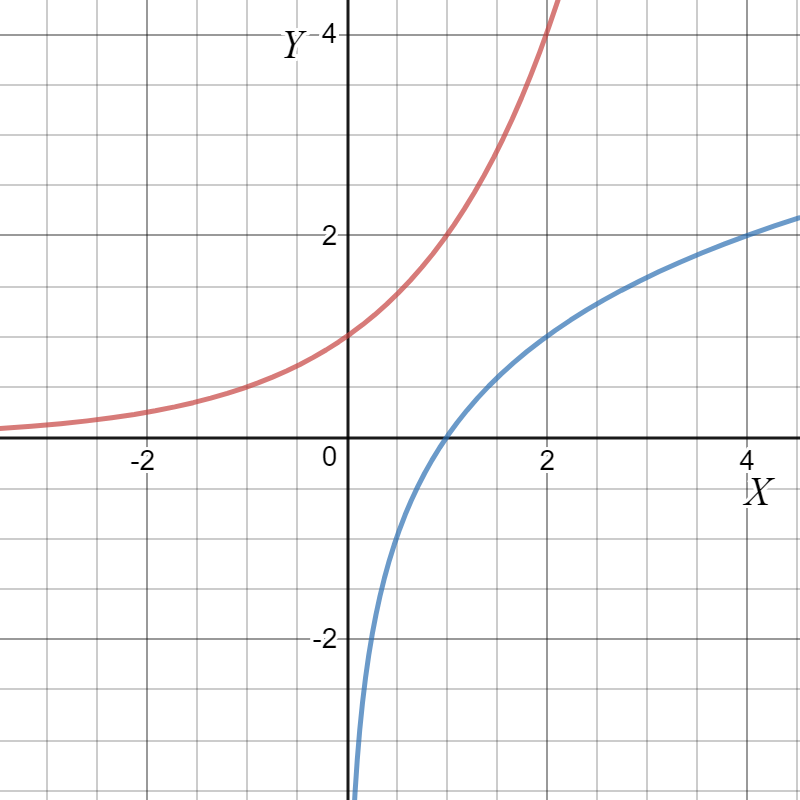
Fig 2: Graph of exponential and logarithmic functions
Comparison of exponential and logarithmic functions
| Property | Exponential | Logarithmic |
|---|---|---|
| Function | $y=b^x,\;b>0,\;b\ne 1$ | $y=\log_b x,\;b>0,\;b\ne 1$ |
| Domain | All real numbers | $x>0$ |
| Range | $y>0$ | All real numbers |
| Intercept | $x=0'\;y=1$ | $x=1\;y=0$ |
| Increasing | When $b>1$ | When $b>1$ |
| Decreasing | When $0<b<1$ | When $0<b<1$ |
Additional resources
- Exponential and Logarithmic Functions - extensive notes on exponential and logarithmic functions
- Notes and exercises - further notes and exercises on exponential and logarithmic functions with applications
Mobile options:

