- Events, Workshops and Programs
- Resources by Discipline
-
Support and Resources by Topic
- - Statistics Help (General)
- - Statistics Help (R Commander)
- - Arithmetic
- - Standard Derivatives
- - Standard Integrals
- - Hyperbolic Trigonometric Functions
- - Remainders and Quotients
- - SPSS Help
- - Logic Basics: AND, OR, NOT
- - Approximations: rounding and truncation
- - Mathematical Terminology
- - Proportional Reasoning
- - Number Sense
- - I Don't Get It
- - Inequalities and relational operators
- - Percentages
- - Help! I can't do it!
- FYiMaths NSW
- About the MESH team
- Contact the MESH team
- MESH Research
- Resources for Staff
Scientific Notation
There are many strategies to convert numbers into scientific notation and to reverse the process. The results are always the same. One strategy is provided in this module.
A number written in scientific notation is written as a number between $1$ and $10$ multiplied by a power of $10$.
To convert numbers into scientific notation:
- Move the decimal point until there is one (non-zero) number in front of the decimal point.
- The exponent of the power of 10 is determined by the number of places you have moved the decimal point.
- If the original number is large, you have moved the decimal point to the left, and the number of places you moved the decimal point is the exponent of the power of 10.
- If the original number is small, you have moved the decimal point to the right, and the exponent of the power of 10 is the negative integer of the number of places you moved the decimal point.
- Put the number in the correct pattern for scientific notation.
Example 1
Write the number $624000$ in scientific notation.

- After moving the decimal point, so the number has one digit in front of the decimal point, the number is $6.24$ (this number is between $1$ and $10$).
- The decimal point has been moved $5$ places to the left so the exponent of the power of $10$ is $5$.
- The number in scientific notation is $6.24\times 10^5$
Example 2
Write $0.000009205$ in scientific notation.

- After moving the decimal point, so the number has one digit in front of the decimal point, the number is $9.205$ (this number is between $1$ and $10$).
- The decimal point has been moved $6$ places to the right so the exponent of the power of $10$ is $-6$.
- The number in scientific notation is $9.205\times 10^{-6}$.
Convert the following numbers to scientific notation. Write your answer so it would appear as $\text{Number}\times 10^{\text{Index}}$.
| Number | Number Index | |
| $3782000$ | ||
| $0.000059$ | ||
| $0.0004052$ | ||
| $73060000$ |
To write numbers without scientific notation we use the reverse process to that used to convert into scientific notation.
The steps are:
- Start with the number between $1$ and $10$.
- Move the decimal point, the number of places moved is the exponent of $10$.
- If the exponent is positive move the decimal point to the right.
- If the exponent is negative move the decimal point to the left.
Example 1
Write $7.53\times 10^7$ without scientific notation.
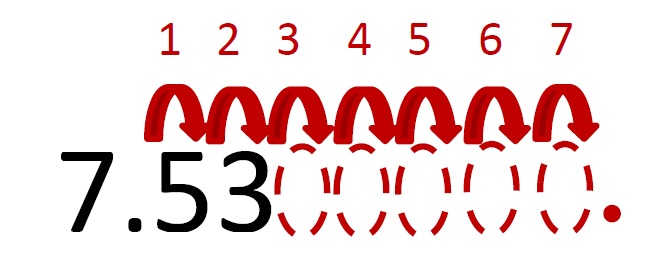
$$7.53\times 10^7 = 75300000.$$
Example 2
Write $3.276\times 10^{-9}$ without scientific notation.
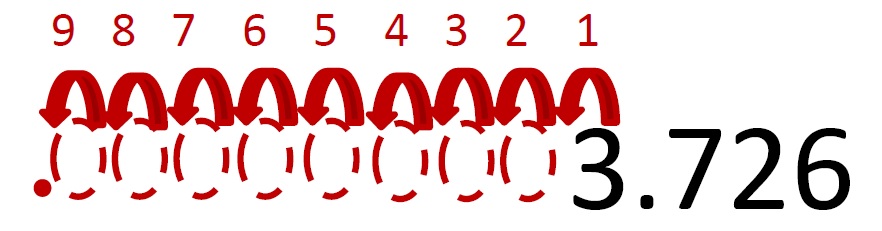
$$3.726\times 10^{-9}=0.000000003726.$$
| $6.4 \times 10^4=$ | ||
| $1.8 \times 10^{-6}=$ | ||
| $4.07 \times 10^{-9}=$ | ||
| $9.006\times 10^9=$ |
Mobile options:

