NMR Pulse Sequences
The following sequences are freely available for use. They have been developed by the Nanoscale Research Group for Bruker systems, although they can be ported to other spectrometer brands. It would be appreciated if you would cite the appropriate reference / references, when using any of the following sequences.
PGSTE-WATERGATE: An STE-based PGSE NMR sequence with excellent solvent suppression
This is a stimulated-echo based pulsed gradient spin-echo NMR diffusion sequence incorporating selective inversion based solvent signal suppression. The sequence provides superb solvent suppression without any phase distortion. The sequence is simple to set up and particularly suited to measuring diffusion coefficients in aqueous solution such as is commonly required in biomolecular NMR experiments (e.g., probing drug-protein interactions).
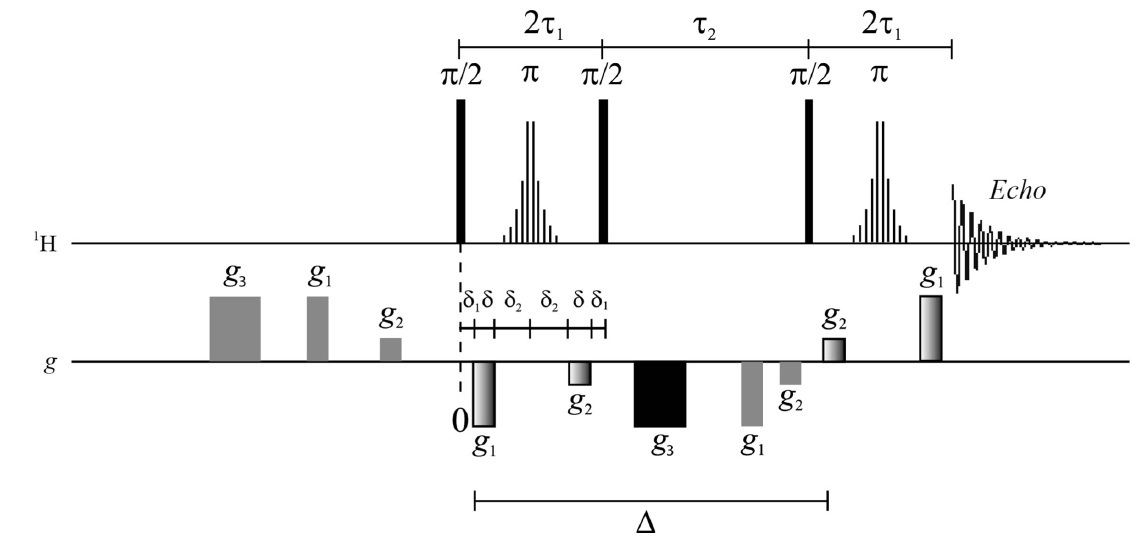
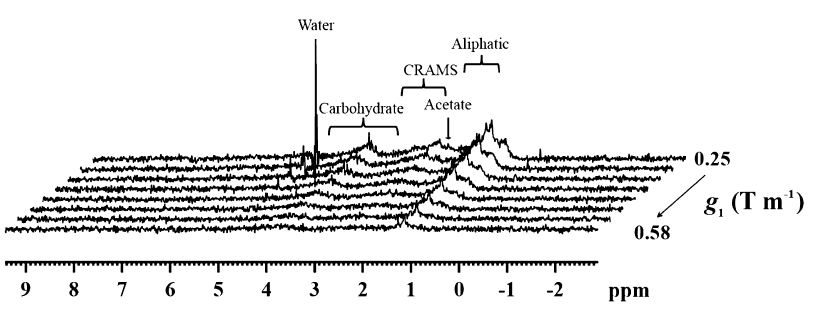
Fig. The modified PGSTE-WATERGATE sequence (top) and the 1H 500 MHz spectra of the un-concentrated pond water obtained using the sequence with different g1 values.
The sequence and other information can be downloaded HERE (DOCX, 13.48 KB)(opens in a new window). The sequence is for a Bruker spectrometer. After downloading the file, copy and paste contents into text file, then follow the instructions below:
Experimental Setup
1. Installation of the Sequence
Copy the TXT file of the pulse sequence into /opt/topspin/exp/stan/nmr/lists/pp/user.
Please note the comments in the sequence.
2. How to set the gradients
At the start of a PGSTE-WATERGATE experiment, the gp1 and gp2 values in the pulse program should be set large enough to suppress the solvent signal with gp1 – gp2 = 0.005 T/m (e.g., gp1 = 0.105 T/m, gp2 = 0.1 T/m, d15 = 100 ms, p20= 4 ms). It is always desirable to have the shortest possible p20 and large enough gp1 and gp2 values in order to minimise the signal loss caused by T2 relaxation.
After reaching the desired solvent suppression level, gp2 should be kept constant and gp1 should be increased with suitable increments to obtain the attenuation curve (e.g., gp1 = 0.105, 0.155, … , 0.505, 0.555 T/m, gp2 = 0.1 T/m). It is convenient to use an ‘au program’ to increase gpz1 from spectrum to spectrum.
N.B., gp1 should be always larger than gp2. This is different from what has been mentioned in our original 2008 paper listed in the Reference section.
3. About d19
The delay “d19” controls the inversion band width (i.e., 1 / (2*d19)) of the selective π pulse. It is usually set between 100 μs to 250 μs depending on the required selectivity of suppression, a longer d19 gives a higher selectivity of suppression. Of course, some resonances at the edges of the spectrum may be attenuated or even obliterated when the selectivity of suppression is being enhanced due to the narrowing of inversion band width.
4. Data analysis
Data analysis is conveniently conducted in a program such as Origin (OriginLab, MA, USA). Here we present the steps for performing an analysis of diffusion data using Origin.
The Origin fitting function (i.e., PGSTEWATERGATE.fdf), which is included in this package, should be copied to the user’s Origin working folder (e.g., C:\Program Files \OriginLab \Origin8 \UserName \fitfunc). After starting Origin, the user should perform the following steps:
- “Tools” --> “Fitting Function Organizer” -->
- Choose “User Defined” directory -->
- Click “New Category” -->
- Give a name to the new category -->
- Click “Add” --> Goes to your working folder and include the new fitting function (i.e., PGSTEWATERGATE.fdf)
- Click “Save” and then “OK”,
- Click “Yes” in the pop-up window.
- After including the new fitting function, the gp1 values (in T/m) should be inserted into the worksheet and used as the “X” column and the normalized attenuation values should be entered as the “Y” column.
- Highlight the “Y” column and then choose “Analysis” -> “Fitting” --> “Nonlinear Curve Fit” --> “Open Dialog”.
- Choose the new fitting function and go to “Parameters”. Except for “A” and “D”, all the “Fixed” boxes should be ticked. The values of the parameters should be filled up: 1 for “A”, the initial value for “D” should be close to the real diffusion coefficient of the molecules of interest, and the values of “delta, delta1, delta2, Bigdelta” should be set according to the parameter settings of the diffusion experiment. You are now able to start fitting your data.
References
- Gang Zheng, Timothy Stait-Gardner, P.G. Anil Kumar, Allan M. Torres, William S. Price. PGSTE-WATERGATE: An STE-based PGSE NMR sequence with excellent solvent suppression. Journal of Magnetic Resonance 191 (2008) 159–163 https://doi.org/10.1016/j.jmr.2007.12.001 (opens in a new window)
- Gang Zheng and William S Price. Direct hydrodynamic radius measurement on dissolved organic matter in natural waters using diffusion NMR. Environmental Science & Technology 46 (2012) 1675 – 1680 https://doi.org/10.1021/es202809e (opens in a new window)
Notes. It would be appreciated if you could cite the reference papers above after utilising the PGSTE-WATERGATE sequence in your research work.
Steady State Pulsed Gradient Spin Echo (SS-PGSE)
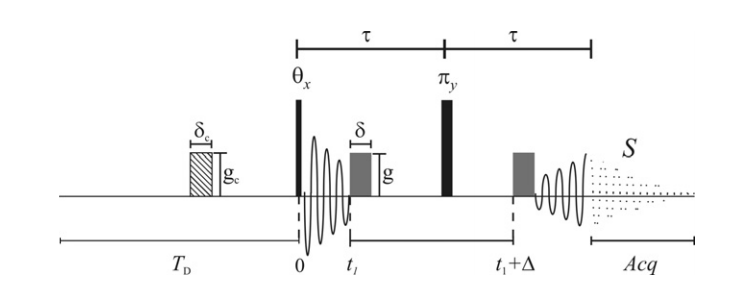 Fig. The Steady State Pulsed Gradient Spin Echo Sequence. Incorporation of the gradient pre-pulse eliminates the need to wait 5T1 after the π pulse.
Fig. The Steady State Pulsed Gradient Spin Echo Sequence. Incorporation of the gradient pre-pulse eliminates the need to wait 5T1 after the π pulse.
The sequence and other information can be downloaded HERE (DOCX, 12.61 KB)(Opens in a new window) The sequence is for a Bruker spectrometer. After downloading the file, copy and paste contents into text file, then follow the instructions below:
Experimental Setup
1. Installation of the sequence
Copy the TXT file of the pulse sequence into /opt/topspin/exp/stan/nmr/lists/pp/user.
2. How to run the sequence and analyse the data
The sequence is very easy to run and analyse, with much of the setup and all the analysis being identical to the PGSE sequence. The only difference from PGSE is the crusher gradient which should be set sufficiently large such that it eliminates any residual transverse magnetisation – three times the area of the maximum diffusion encoding gradients should be enough. The recycle delay can be reduced, sometimes significantly while taking into account the caveats in [1, 2].
Data analysis is also simple, being identical to PGSE, which involves fitting an exponential (A exp(–γ2g2δ2D(Δ – δ/3)) with A and D the fitting parameters) to obtain the diffusion coefficient D. Further details can be found in [1,2].
References
1. T. Stait-Gardner, P.G.A. Kumar, W.S. Price, Steady state effects in PGSE NMR diffusion experiments, Chem. Phys. Lett., 462 (2008) 331-336. https://doi.org/10.1063/1.4918279 (opens in a new window)
2. M. Zubkov, T. Stait-Gardner, W.S. Price, P. Stilbs, Steady state effects in a two-pulse diffusion-weighted sequence, J. Chem. Phys., 142 (2015). https://doi.org/10.1063/1.4918279 (opens in a new window)
Note. It would be appreciated if you could cite the paper above after using the SS-PGSE sequence in your research work.
J Compensated Pulsed Gradient Stimulated Echo (PGSE)
The J-compensated pulsed gradient spin-echo sequence or J-PGSE [1] was introduced by our group in 2010 in order to eliminate peak distortion and spin-spin coupling modulation in NMR diffusion pulsed gradient spin-echo (PGSE) experiments (Fig. 1). The double spin-echo component of the J-PGSE refocuses homonuclear spin-spin coupling evolution so that peaks appear in-phase. This J-compensated double echo operates in a similar fashion to the perfect echo sequence that was introduced by Takegoshi and co-workers [2] in 1989 and by van Zijl et al [3] in 1990. 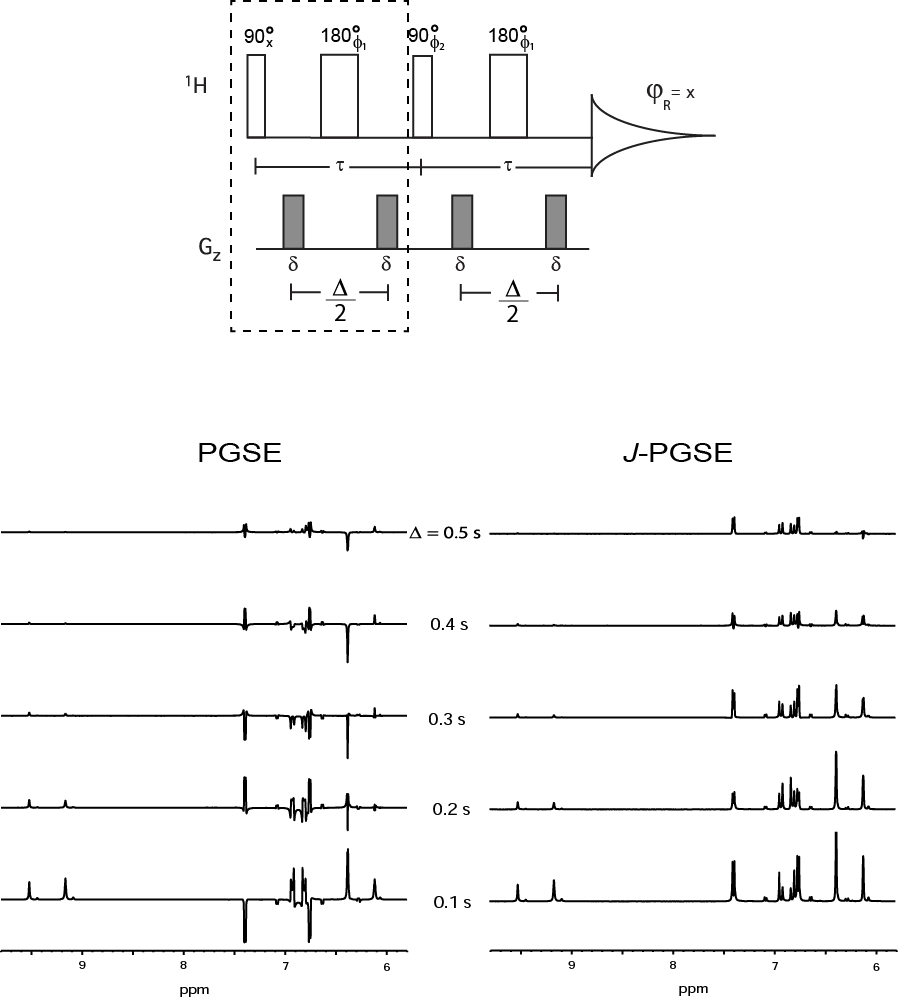 Fig 1. The J-PGSE pulse sequence (top) and 1H resveratrol spectra comparing the regular (PGSE) and compensated (J-PGSE) sequences acquired at 400 MHz. The dashed rectangle indicates the regular PGSE pulse sequence which is repeated in the J-PGSE sequence.
Fig 1. The J-PGSE pulse sequence (top) and 1H resveratrol spectra comparing the regular (PGSE) and compensated (J-PGSE) sequences acquired at 400 MHz. The dashed rectangle indicates the regular PGSE pulse sequence which is repeated in the J-PGSE sequence.
References
- A.M. Torres, G. Zheng, W.S.Price. J‐compensated PGSE: an improved NMR diffusion experiment with fewer phase distortions (2010) Mag. Res. Chem. 48(2) 129-133 https://doi.org/10.1002/mrc.2555 (opens in a new window)
- K. Takegoshi, K.Ogura, K. Hikichi. A perfect spin echo in a weakly homonuclear J-coupled two spin-12 system. (1969) J.Mag.Res., 84(3) 611-615 https://doi.org/10.1016/0022-2364(89)90127-3 (opens in a new window)
- P.C.M van Zijl, C.T.W Moonen, M von Kienlin. Homonuclear J refocusing in echo spectroscopy (1969) J.Mag.Res., 89 28-40 https://doi.org/10.1016/0022-2364(90)90159-7 (opens in a new window)
PGSE-WATERGATE: A Spin-Echo-based PGSE NMR sequence with excellent solvent suppression
This is a pulsed gradient spin-echo NMR diffusion sequence incorporating WATERGATE-based solvent signal suppression [1,2]. The sequence provides superb solvent suppression without phase distortion. The sequence is easy to set up and particularly robust with respect to parameter settings. Since it is based on a spin-echo, the sequence is especially suited to measuring the diffusion coefficients of small molecules in low viscosity solutions such as is commonly required in biomolecular NMR experiments (e.g., probing ligand-protein interactions by measuring the ligand diffusion coefficient). This version of the pulse sequence computes sets the variable delays to give the shortest pulse sequence and therefore echo time (τ) delays. A more complicated variant is available which allows particularτ values to be set.
For cases where T1 >> T2 or a suitable value of the echo time (τ) cannot be found to overcome the deleterious effects of J-modulation effects the PGSTE-WATERGATE sequence is preferable.
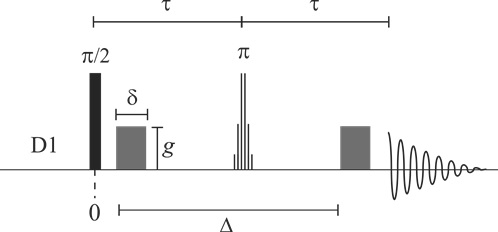
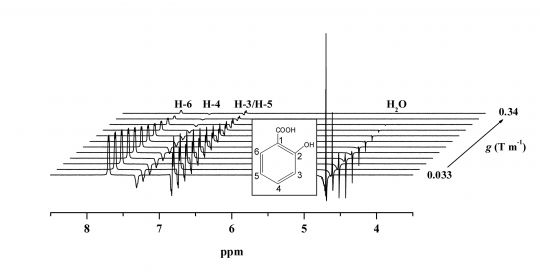
Experimental Setup
1. Installation of the Sequence
Copy the TXT file of the pulse sequence into /opt/topspin/exp/stan/nmr/lists/pp/user.
Please note the comments in the sequence.
2. How to run the sequence and analyse the data
The PGSE-WATERGATE experiment is run like a standard PGSE sequence in that suitable values of Δ and δ are chosen so that the signal will be almost completely attenuated at the maximum value of g used (input using gpz1). It is convenient to use an ‘au program’ to increase gpz1 from spectrum to spectrum. A simple modification allows this to be run in ‘2D’ mode.
Data analysis simply involves fitting an exponential A exp(–γ2g2δ2D(Δ – δ/3) (with A and D the fitting parameters) to obtain the diffusion coefficient D. Further details can be found in [3].
References
[1] Price, W. S.; Elwinger, F.; Vigouroux, C.; Stilbs, P., PGSE-WATERGATE, a New Tool for NMR Diffusion-Based Studies of Ligand-Macromolecule Binding. Magn. Reson. Chem. 2002, 40 (6), 391-395.
(https://doi.org/10.1002/mrc.1029)
[2] Price, W. S., Pulsed Field Gradient NMR as a Tool for Studying Translational Diffusion, Part I. Basic Theory. Concepts Magn. Reson. 1997, 9 (5), 299-336.
(https://doi.org/10.1002/(SICI)1099-0534(1997)9:5%3C299::AID-CMR2%3E3.0.CO;2-U)
[3] Price, W. S., Pulsed Field Gradient NMR as a Tool for Studying Translational Diffusion, Part II. Experimental Aspects. Concepts Magn. Reson. 1998, 10 (4), 197-237.
(https://doi.org/10.1002/(SICI)1099-0534(1998)10:4%3C197::AID-CMR1%3E3.0.CO;2-S)
Mobile options:

