Proportional Reasoning Methods

Method 1: Write and solve a proportion equation

Example 1

If $1000$ lines of code can be executed in $15$ seconds, how many lines of code can be executed in $9$ seconds?

Steps

1: Write an equation:

The required proportion is $1000$ lines/$15$ sec.

Find the number of lines executed in $9$ seconds so that the proportion stays the same.

Equate the two proportions:

$1000$ lines/$15$ sec = _____ lines/$9$ sec.

We usually let $x$ be the number of lines that we are looking for. hence the equation above can be written as: $$\frac{1000}{15}=\frac{x}{9}$$

2: Now we can solve for $x$: \begin{align*} \frac{1000}{15}&=\frac{x}{9}\\[1ex] 9000&=15x\\ x&=600 \end{align*}

Therefore, $600$ lines of code can be executed in $9$ seconds.

Example 2

A rectangular image is enlarged so the its length changes from $6$ cm to $80$ cm. If the original width of the image is $15$ cm, what is the width of the enlarged image if the image stays in the original proportion (that is it is enlarged without distortion)?

If the image is enlarged without distortion, the ratio of the original length to enlarged length is equal to the ratio of original with to enlarged width. We can write this as an equation, where the missing value (the enlarged width) is represented by $x$.

original length : enlarged length = original width : enlarged width

$6$ cm:$80$ cm = $15$ cm:____cm \begin{align*} 6:80&=15:x\\\frac{6}{80}&=\frac{15}{x}\\[1ex]\frac{6x}{80}&=15\\[1ex] 6x&=1200\\x&=200\end{align*}

Therefore, the width of the enlarged image is $200$ cm.

Method 2: Unitary method

Example

If $1000$ lines of code can be executed in $15$ seconds, how many lines of code can be executed in $9$ seconds?

Note that 'unit' means one.

Find how many lines of code can be executed in $1$ second, then multiply to find the required amount in $9$ seconds.

Steps

1: Convert the proportion to lines of code executed in $1$ second.

The proportion is $1000$ lines of code for each $15$ seconds.

$1000\text{ lines}\div 15\quad\text{and}\quad 15\text{ seconds}\div 15$

So $\displaystyle{\frac{1000}{15}}$ lines are executed in each one second.

2: We now know that $\displaystyle{\frac{1000}{15}}$ lines of code are executed in each one second.

$\frac{1000}{15}\text{ lines}\times 9\quad\text{and}\quad 1\text{ second}\times 9$

So $600$ lines ($1000\div 15\times 9$) of code can be executed in $9$ seconds.

Method 3: Use a table to build up to the required amount by multiplying and/or dividing

Example

If $1000$ lines of code can be executed in $15$ seconds, how many lines of code can be executed in $9$ seconds?

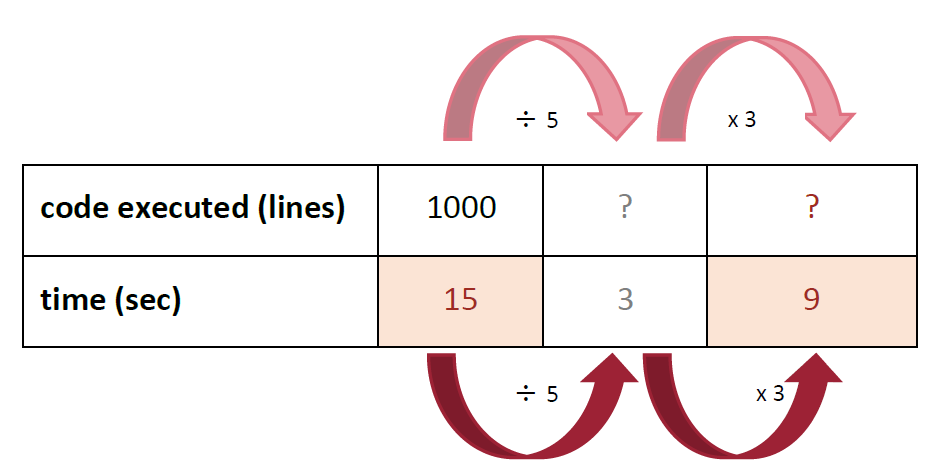
Use the table to build up or down from $15$ to $9$ using only $\div$ and $\times$ (shown with red arrows).

$15\text{ sec}\div 5\times 3= 9\text{ sec}$

Then: repeat the same operations for code ($1000\div 5\times 3$)(shown with pink arrows).

Alternatively:

Tip: If you are comfortable using fractions you could think of $\div 5\times 3$ as just $\displaystyle{\times\frac35}$.

Now try these questions to practise your proportional reasoning skills.