- Events, Workshops and Programs
- Resources by Discipline
-
Support and Resources by Topic
- - Statistics Help (General)
- - Statistics Help (R Commander)
- - Arithmetic
- - Standard Derivatives
- - Standard Integrals
- - Hyperbolic Trigonometric Functions
- - Remainders and Quotients
- - SPSS Help
- - Logic Basics: AND, OR, NOT
- - Approximations: rounding and truncation
- - Mathematical Terminology
- - Proportional Reasoning
- - Number Sense
- - I Don't Get It
- - Percentages
- Contact the MESH team
- MESH Research
- Resources for Staff
More on comparing size of integers
Integers can be represented as equally spaced points on a number line. The horizontal number line is drawn below.
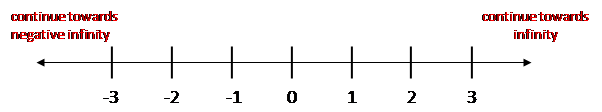
Did you notice that the numbers to the left of zero have negative signs in front of them?
Important
Numbers to the right of zero are called 'positive' numbers: $+1, +2, +3, +4$, and so on. We don't usually write or say the positive sign, unless it's really needed to communicate clearly.
Numbers to the left of zero are called 'negative' numbers: $-1, -2, -3, -4$, and so on. We always write and say the negative sign $(-)$ to communicate clearly.
The number zero is neither negative nor positive.
Example
Examples where negative integers are used include temperatures below zero degrees, money transactions where you owe more than you receive, moving in a backward direction, elevations below sea level, and golf scores below par.
A temperature of $-15$ degrees Celsius is colder than a temperature of $-3$ degrees Celsius. So $-15$ is more negative, and so smaller than, $-3$.
Important
When comparing the size of two integers think about where they are on the number line:
- we say the number furthest to the right is largest
- we say the number furthest to the left is smallest.
So:
- $1$ is greater than $-2$, also written as $1 \gt -2$. On the number line $1$ is to the right of $-2$.
- $-3$ is smaller than $-1$, also written as $-3 \lt -1$. On the number line $-3$ is to the left of $-1$.
| Is $-3$ greater than $2$? | |
| Is $-2$ smaller than $-1$? |
Mobile options:

